从最长回文子串问题引发的后缀树思考

发表于 | 更新于 | 分类于

最近碰到一个求解最长回文子串的问题，即给定一个字符串s，需要找到s中最长的回文子串。例如：

  • 输入: “babad”
  • 输出: “bab” （注意”aba”也是一个有效答案)

这个题目的解法有多种。一般来说比较流行的是 动态规划 或者 最长公共子串 法。

动态规划

首先讲一下动态规划的方法。这里主要是利用回文数的性质来做的。给出以下定义：

$$
P(i,j) =
\begin{cases}
true & 如果 s[i,j] 是回文子串 \\
false & 如果 s[i,j]不是回文子串
\end{cases}
$$
那么利用动态规划，我们可以得到状态转移式：
$$
P(i,j) = (P(i+1,j-1) \&\& (S_i == S_j))
$$
所以在求解最长回文子串的过程中，我们只需要维护类型为boolean的dp[i][j]数组，其意义如下：
$$
boolean[i][j] =
\begin{cases}
true & 如果s[i:j]是回文串 \\
false & 如果s[i:j]不是回文串
\end{cases}
$$
初始化该数组后，我们依次对长度为1，2，…，len-1长度的子串进行遍历，填充boolean数组，并且在填充的过程中，记录最长子串的位置即可。具体来说：

  1. 遍历长度为1的子串，即boolean[i][i]，全部初始化为true。
  2. 遍历长度为2的子串，boolean[i][i+1] = (s[i] == s[i+1]).
  3. 依次遍历长度为3，4，…，len-1的子串，利用动态规划的性质。

遍历完毕后，即得到最长回文子串的位置。

下面分析该方法的时间复杂度和空间复杂度：

  1. 时间复杂度：两层遍历，外层长度为n，内层依次为n, n-1, n-1, …, 1. 故时间复杂度为$O(n^2)$.
  2. 空间复杂度：维护数组dp[n][n]，故空间复杂度为$O(n^2)$.

下面附上代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public String longestPalindrome(String s) {
    if (s == null || s.length() == 0)
        return "";
    int len = s.length(); 
    boolean[][] dp = new boolean[len][len];  //default to false.
    int max = 1;
    int start = 0;
    for (int i = 0; i < len-1; i++) {
        dp[i][i] = true;
        dp[i+1][i] = true;
    }
    dp[len-1][len-1] = true;

    for (int k = 1; k <= len; k++) {
        for (int i = 0; i + k < len; i++) {
            if (s.charAt(i) == s.charAt(i+k) && dp[i+1][i+k-1]) {
                dp[i][i+k] = true;
                if (k+1 > max) {
                    max = k+1;
                    start = i;
                }
            }
        }
    }
    return s.substring(start, start+max);
}

中心扩展

中心扩展的方法，同样利用了动态规划的思想，但是在其基础上，进行了改进。

中心扩展的思路如下：

  1. 对于长度为n的字符串s，找到其2n个中点。
  2. 对每一个中点，往两边扩展找到最长的回文子串。
  3. 所有中点遍历完后，即找到最长的回文子串。

注意：有2n个中点是因为回文子串既有偶数也有奇数形式，对于奇数形式我们定义其中点为中心字符，对于偶数形式我们定义其中点为中心两个字符之间的中点。

用java对以上方法进行实现，得到以下代码：

LongestPalindrome.java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
public class LongestPalindrome {
    /**
     * Find the longest palindrome of s.
     */
    public String longestPalindrome(String s) {
        int len = s.length();
        int max = 0;
        int center = 0;
        for (int i = 0; i < len; i++) {
            int l1 = palindromeFrom(s, len, i, i);
            int l2 = palindromeFrom(s, len, i, i+1);
            int ml = Math.max(l1, l2);
            if  (ml > max) {
                max = ml;
                center = i;
            }
        }
        int left = center - (max - 1) / 2;
        int right = center + max / 2;
        return s.substring(left, right+1);
    }

    /**
     * find the longest palindrome of s from center: (left + right) / 2.
     */
    private int palindromeFrom(String s, int len, int left, int right) {
        if (left == right) {
            int result = 1;
            left--;right++;
            while(left >= 0 && right < len && s.charAt(left) == s.charAt(right)) {
                result += 2;
                left--;right++;
            }
            return result;
        }
        else {
            int result = 0;
            while(left >= 0 && right < len && s.charAt(left) == s.charAt(right)) {
                result += 2;
                left--;right++;
            }
            return result;
        }
    }


    public static void main(String[] args) {
        LongestPalindrome longestPalindrome = new LongestPalindrome();
        System.out.println(longestPalindrome.longestPalindrome("babad"));
    }
}

后缀树

以下是由字符串ABAB, BABA, ABBA组成的广义后缀树。

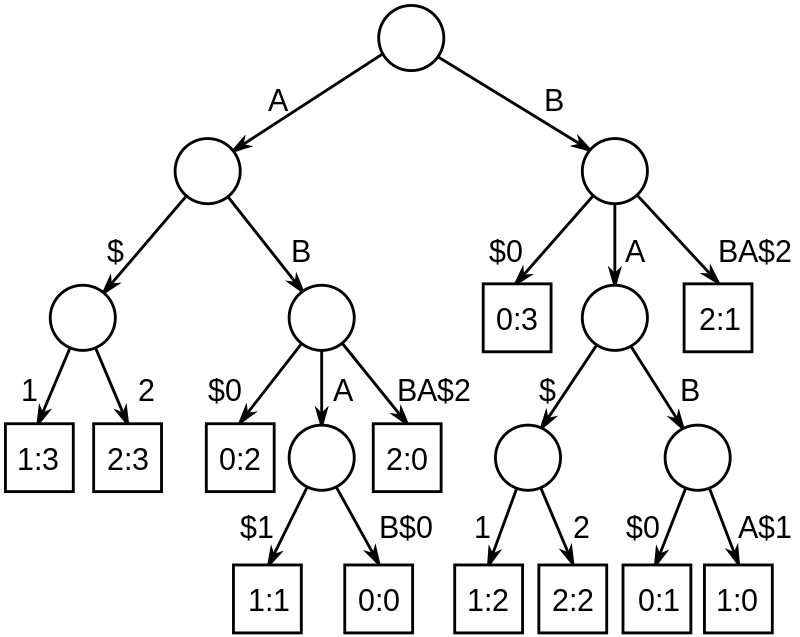
下面对后缀树进行一个解释。